Optimization and Regression

Classes
class	LeastAngleRegressionOptions
	Pass options to leastAngleRegression(). More...
class	NonlinearLSQOptions
	Pass options to nonlinearLeastSquares(). More...

Functions
template<... >
unsigned int	leastAngleRegression (...)
template<class T , class C1 , class C2 , class C3 >
bool	leastSquares (MultiArrayView< 2, T, C1 > const &A, MultiArrayView< 2, T, C2 > const &b, MultiArrayView< 2, T, C3 > &x, std::string method="QR")
template<... >
void	nonlinearLeastSquares (...)
	Fit a non-linear model to given data by minimizing least squares loss. More...
template<... >
unsigned int	nonnegativeLeastSquares (...)
template<... >
unsigned int	quadraticProgramming (...)
template<class T , class C1 , class C2 , class C3 >
bool	ridgeRegression (MultiArrayView< 2, T, C1 > const &A, MultiArrayView< 2, T, C2 > const &b, MultiArrayView< 2, T, C3 > &x, double lambda)
template<class T , class C1 , class C2 , class C3 , class Array >
bool	ridgeRegressionSeries (MultiArrayView< 2, T, C1 > const &A, MultiArrayView< 2, T, C2 > const &b, MultiArrayView< 2, T, C3 > &x, Array const &lambda)
template<class T , class C1 , class C2 , class C3 , class C4 >
bool	weightedLeastSquares (MultiArrayView< 2, T, C1 > const &A, MultiArrayView< 2, T, C2 > const &b, MultiArrayView< 2, T, C3 > const &weights, MultiArrayView< 2, T, C4 > &x, std::string method="QR")
template<class T , class C1 , class C2 , class C3 , class C4 >
bool	weightedRidgeRegression (MultiArrayView< 2, T, C1 > const &A, MultiArrayView< 2, T, C2 > const &b, MultiArrayView< 2, T, C3 > const &weights, MultiArrayView< 2, T, C4 > &x, double lambda)

Detailed Description

Function Documentation

unsigned int vigra::quadraticProgramming

(

...

)

Solve Quadratic Programming Problem.

The quadraticProgramming() function implements the algorithm described in

D. Goldfarb, A. Idnani: "A numerically stable dual method for solving strictly convex quadratic programs", Mathematical Programming 27:1-33, 1983.

for the solution of (convex) quadratic programming problems by means of a primal-dual method.

#include <vigra/quadprog.hxx>
Namespaces: vigra

Declaration:

namespace vigra { 
    template <class T, class C1, class C2, class C3, class C4, class C5, class C6, class C7>
    T 
    quadraticProgramming(MultiArrayView<2, T, C1> const & GG, MultiArrayView<2, T, C2> const & g,  
                         MultiArrayView<2, T, C3> const & CE, MultiArrayView<2, T, C4> const & ce,  
                         MultiArrayView<2, T, C5> const & CI, MultiArrayView<2, T, C6> const & ci, 
                         MultiArrayView<2, T, C7> & x);
}

The problem must be specified in the form:

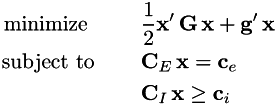
Matrix G G must be symmetric positive definite, and matrix C_E must have full row rank. Matrix and vector dimensions must be as follows:

• G: [n * n], g: [n * 1]
• C_E: [me * n], c_e: [me * 1]
• C_I: [mi * n], c_i: [mi * 1]
• x: [n * 1]

The function writes the optimal solution into the vector x and returns the cost of this solution. If the problem is infeasible, std::numeric_limits::infinity() is returned. In this case the value of vector x is undefined.

Usage:

Minimize f = 0.5 * x'*G*x + g'*x subject to -1 <= x <= 1. The solution is x' = [1.0, 0.5, -1.0] with f = -22.625.

double Gdata[] = {13.0, 12.0, -2.0,
                  12.0, 17.0,  6.0,
                  -2.0,  6.0, 12.0};

double gdata[] = {-22.0, -14.5, 13.0};

double CIdata[] = { 1.0,  0.0,  0.0,
                    0.0,  1.0,  0.0,
                    0.0,  0.0,  1.0,
                   -1.0,  0.0,  0.0,
                    0.0, -1.0,  0.0,
                    0.0,  0.0, -1.0};
                  
double cidata[] = {-1.0, -1.0, -1.0, -1.0, -1.0, -1.0};

Matrix<double> G(3,3, Gdata), 
               g(3,1, gdata), 
               CE,             // empty since there are no equality constraints
               ce,             // likewise
               CI(7,3, CIdata), 
               ci(7,1, cidata), 
               x(3,1);
             
double f = quadraticProgramming(G, g, CE, ce, CI, ci, x);

This algorithm can also be used to solve non-negative least squares problems (see nonnegativeLeastSquares() for an alternative algorithm). Consider the problem to minimize f = (A*x - b)' * (A*x - b) subject to x >= 0. Expanding the product in the objective gives f = x'*A'*A*x - 2*b'*A*x + b'*b. This is equivalent to the problem of minimizing fn = 0.5 * x'*G*x + g'*x with G = A'*A and g = -A'*b (the constant term b'*b has no effect on the optimal solution and can be dropped). The following code computes the solution x' = [18.4493, 0, 4.50725]:

double A_data[] = {
     1, -3,  2,
    -3, 10, -5,
     2, -5,  6
};

double b_data[] = {
     27, 
    -78, 
     64
};

Matrix<double> A(3, 3, A_data),
               b(3, 1, b_data),
               G =   transpose(A)*A,
               g = -(transpose(A)*b),
               CE,    // empty since there are no equality constraints
               ce,    // likewise
               CI = identityMatrix<double>(3), // constrain all elements of x
               ci(3, 1, 0.0),                  // ... to be non-negative
               x(3, 1);

quadraticProgramming(G, g, CE, ce, CI, ci, x);

Examples:

nnlsq.cxx.

bool vigra::linalg::leastSquares	(	MultiArrayView< 2, T, C1 > const &	A,
		MultiArrayView< 2, T, C2 > const &	b,
		MultiArrayView< 2, T, C3 > &	x,
		std::string	method = "QR"
	)

Ordinary Least Squares Regression.

Given a matrix A with m rows and n columns (with m >= n), and a column vector b of length m rows, this function computes the column vector x of length n rows that solves the optimization problem

When b is a matrix with k columns, x must also have k columns, which will contain the solutions for the corresponding columns of b. Note that all matrices must already have the correct shape.

This function is just another name for linearSolve(), perhaps leading to more readable code when A is a rectangular matrix. It returns false when the rank of A is less than n. See linearSolve() for more documentation.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

bool vigra::linalg::weightedLeastSquares	(	MultiArrayView< 2, T, C1 > const &	A,
		MultiArrayView< 2, T, C2 > const &	b,
		MultiArrayView< 2, T, C3 > const &	weights,
		MultiArrayView< 2, T, C4 > &	x,
		std::string	method = "QR"
	)

Weighted Least Squares Regression.

Given a matrix A with m rows and n columns (with m >= n), a vector b of length m, and a weight vector weights of length m with non-negative entries, this function computes the vector x of length n that solves the optimization problem

where diag(weights) creates a diagonal matrix from weights. The algorithm calls leastSquares() on the equivalent problem

where the square root of weights is just taken element-wise.

When b is a matrix with k columns, x must also have k columns, which will contain the solutions for the corresponding columns of b. Note that all matrices must already have the correct shape.

The function returns false when the rank of the weighted matrix A is less than n.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

bool vigra::linalg::ridgeRegression	(	MultiArrayView< 2, T, C1 > const &	A,
		MultiArrayView< 2, T, C2 > const &	b,
		MultiArrayView< 2, T, C3 > &	x,
		double	lambda
	)

Ridge Regression.

Given a matrix A with m rows and n columns (with m >= n), a vector b of length m, and a regularization parameter lambda >= 0.0, this function computes the vector x of length n that solves the optimization problem

This is implemented by means of singularValueDecomposition().

When b is a matrix with k columns, x must also have k columns, which will contain the solutions for the corresponding columns of b. Note that all matrices must already have the correct shape.

The function returns false if the rank of A is less than n and lambda == 0.0.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

bool vigra::linalg::weightedRidgeRegression	(	MultiArrayView< 2, T, C1 > const &	A,
		MultiArrayView< 2, T, C2 > const &	b,
		MultiArrayView< 2, T, C3 > const &	weights,
		MultiArrayView< 2, T, C4 > &	x,
		double	lambda
	)

Weighted ridge Regression.

Given a matrix A with m rows and n columns (with m >= n), a vector b of length m, a weight vector weights of length m with non-negative entries, and a regularization parameter lambda >= 0.0 this function computes the vector x of length n that solves the optimization problem

where diag(weights) creates a diagonal matrix from weights. The algorithm calls ridgeRegression() on the equivalent problem

where the square root of weights is just taken element-wise. This solution is computed by means of singularValueDecomposition().

When b is a matrix with k columns, x must also have k columns, which will contain the solutions for the corresponding columns of b. Note that all matrices must already have the correct shape.

The function returns false if the rank of A is less than n and lambda == 0.0.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

bool vigra::linalg::ridgeRegressionSeries	(	MultiArrayView< 2, T, C1 > const &	A,
		MultiArrayView< 2, T, C2 > const &	b,
		MultiArrayView< 2, T, C3 > &	x,
		Array const &	lambda
	)

Ridge Regression with many lambdas.

This executes ridgeRegression() for a sequence of regularization parameters. This is implemented so that the singularValueDecomposition() has to be executed only once. lambda must be an array conforming to the std::vector interface, i.e. must support lambda.size() and lambda[k]. The columns of the matrix x will contain the solutions for the corresponding lambda, so the number of columns of the matrix x must be equal to lambda.size(), and b must be a columns vector, i.e. cannot contain several right hand sides at once.

The function returns false when the matrix A is rank deficient. If this happens, and one of the lambdas is zero, the corresponding column of x will be skipped.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

unsigned int vigra::linalg::leastAngleRegression

(

...

)

Least Angle Regression.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

Declarations:

namespace vigra {
   namespace linalg {
     // compute either LASSO or least squares solutions
     template <class T, class C1, class C2, class Array1, class Array2>
     unsigned int
     leastAngleRegression(MultiArrayView<2, T, C1> const & A, MultiArrayView<2, T, C2> const &b,
              Array1 & activeSets, Array2 & solutions,
              LeastAngleRegressionOptions const & options = LeastAngleRegressionOptions());

     // compute LASSO and least squares solutions
     template <class T, class C1, class C2, class Array1, class Array2>
     unsigned int
     leastAngleRegression(MultiArrayView<2, T, C1> const & A, MultiArrayView<2, T, C2> const &b,
              Array1 & activeSets, Array2 & lasso_solutions, Array2 & lsq_solutions,
              LeastAngleRegressionOptions const & options = LeastAngleRegressionOptions());
   }
   using linalg::leastAngleRegression;
}

This function implements Least Angle Regression (LARS) as described in

        B.Efron, T.Hastie, I.Johnstone, and R.Tibshirani: "Least Angle Regression", Annals of Statistics 32(2):407-499, 2004.

It is an efficient algorithm to solve the L1-regularized least squares (LASSO) problem

and the L1-regularized non-negative least squares (NN-LASSO) problem

where A is a matrix with m rows and n columns (often with m < n), b a vector of length m, and a regularization parameter s >= 0.0. L1-regularization has the desirable effect that it causes the solution x to be sparse, i.e. only the most important elements in x (called the active set) have non-zero values. The key insight of the LARS algorithm is the following: When the solution vector x is considered as a function of the regularization parameter s, then x(s) is a piecewise linear function, i.e. a polyline in n-dimensional space. The knots of the polyline x(s) are located precisely at those values of s where one variable enters or leaves the active set and can be efficiently computed.

Therefore, leastAngleRegression() returns the entire solution path as a sequence of knot points, starting at 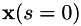(where the only feasible solution is obviously x = 0) and ending at 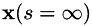(where the solution becomes the ordinary least squares solution). Actually, the initial null solution is not explicitly returned, i.e. the sequence starts at the first non-zero solution with one variable in the active set. The function leastAngleRegression() returns the number of solutions (i.e. knot points) computed.

The sequences of active sets and corresponding variable weights are returned in activeSets and solutions respectively. That is, activeSets[i] is an ArrayVector<int> containing the indices of the variables that are active at the i-th knot, and solutions is a Matrix<T> containing the weights of those variables, in the same order (see example below). Variables not contained in activeSets[i] are zero at this solution.

The behavior of the algorithm can be adapted by LeastAngleRegressionOptions:

options.lasso() (active by default)

Compute the LASSO solution as described above.

options.nnlasso() (inactive by default)

Compute non-negative LASSO solutions, i.e. use the additional constraint that x >= 0 in all solutions.

options.lars() (inactive by default)

Compute a solution path according to the plain LARS rule, i.e. never remove a variable from the active set once it entered.

options.leastSquaresSolutions(bool) (default: true)

Use the algorithm mode selected above to determine the sequence of active sets, but then compute and return an ordinary (unconstrained) least squares solution for every active set.
Note: The second form of leastAngleRegression() ignores this option and does always compute both constrained and unconstrained solutions (returned in lasso_solutions and lsq_solutions respectively).

maxSolutionCount(unsigned int n) (default: n = 0, i.e. compute all solutions)

Compute at most n solutions.

Usage:

int m = ..., n = ...;
Matrix<double> A(m, n), b(m, 1);
... // fill A and b

// normalize the input
Matrix<double> offset(1,n), scaling(1,n);
prepareColumns(A, A, offset, scaling, DataPreparationGoals(ZeroMean|UnitVariance));
prepareColumns(b, b, DataPreparationGoals(ZeroMean));

// arrays to hold the output
ArrayVector<ArrayVector<int> > activeSets;
ArrayVector<Matrix<double> > solutions;

// run leastAngleRegression() in non-negative LASSO mode
int numSolutions = leastAngleRegression(A, b, activeSets, solutions,
                            LeastAngleRegressionOptions().nnlasso());

// print results
Matrix<double> denseSolution(1, n);
for (MultiArrayIndex k = 0; k < numSolutions; ++k)
{
    // transform the sparse solution into a dense vector
    denseSolution.init(0.0); // ensure that inactive variables are zero
    for (unsigned int i = 0; i < activeSets[k].size(); ++i)
    {
        // set the values of the active variables;
        // activeSets[k][i] is the true index of the i-th variable in the active set
        denseSolution(0, activeSets[k][i]) = solutions[k](i,0);
    }

    // invert the input normalization
    denseSolution = denseSolution * pointWise(scaling);

    // output the solution
    std::cout << "solution " << k << ":\n" << denseSolution << std::endl;
}

Required Interface:

• T must be numeric type (compatible to double)
• Array1 a1;
a1.push_back(ArrayVector<int>());
• Array2 a2;
a2.push_back(Matrix<T>());

unsigned int vigra::linalg::nonnegativeLeastSquares

(

...

)

Non-negative Least Squares Regression.

Given a matrix A with m rows and n columns (with m >= n), and a column vector b of length m rows, this function computes a column vector x of length n with non-negative entries that solves the optimization problem

Both b and x must be column vectors (i.e. matrices with 1 column). Note that all matrices must already have the correct shape. The solution is computed by means of leastAngleRegression() with non-negativity constraint.

#include <vigra/regression.hxx>
Namespaces: vigra and vigra::linalg

Declarations:

namespace vigra {
    namespace linalg {
        template <class T, class C1, class C2, class C3>
        void
        nonnegativeLeastSquares(MultiArrayView<2, T, C1> const & A,
                                MultiArrayView<2, T, C2> const &b, 
                                MultiArrayView<2, T, C3> &x);
    }
    using linalg::nonnegativeLeastSquares;
}

Examples:

nnlsq.cxx.

void vigra::nonlinearLeastSquares

(

...

)

Fit a non-linear model to given data by minimizing least squares loss.

Declarations:

namespace vigra {
    // variant 1: optimize a univariate model ('x' is a 1D array of scalar data points)
    template <class T, class S1, class S2, 
              class U, int N, 
              class Functor>
    T
    nonlinearLeastSquares(MultiArrayView<1, T, S1> const & x,
                          MultiArrayView<1, T, S2> const & y,
                          TinyVector<U, N> & model_parameters, 
                          Functor model,
                          NonlinearLSQOptions const & options = NonlinearLSQOptions());

    // variant 2: optimize a multivariate model ('x' is a 2D array of vector-valued data points)
    template <class T, class S1, class S2, 
              class U, int N, 
              class Functor>
    T
    nonlinearLeastSquares(MultiArrayView<2, T, S1> const & x,
                          MultiArrayView<1, T, S2> const & y,
                          TinyVector<U, N> & model_parameters, 
                          Functor model,
                          NonlinearLSQOptions const & options = NonlinearLSQOptions());
}

This function implements the Levenberg-Marquardt algorithm to fit a non-linear model to given data. The model depends on a vector of parameters p which are to be choosen such that the least-squares residual between the data and the model's predictions is minimized according to the objective function:

where 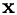is the model to be optimized (with arguments 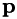and parameters 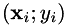), and 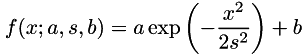are the feature/response pairs of the given data. Since the model is non-linear (otherwise, you should use ordinary leastSquares()), it must be linearized in terms of a first-order Taylor expansion, and the optimal parameters p have to be determined iteratively. In order for the iterations to converge to the desired solution, a good initial guess on p is required.

The model must be specified by a functor which takes one of the following forms:

typedef double DataType;   // type of your data samples, may be any numeric type
static const int N = ...;  // number of model parameters

// variant 1: the features x are scalars
struct UnivariateModel 
{
    template <class T>
    T operator()(DataType x, TinyVector<T, N> const & p) const { ... }
};

// variant 2: the features x are vectors
struct MultivariateModel
{
    template <class T>
    T operator()(MultiArrayView<1, DataType> const & x, TinyVector<T, N> const & p) const { ... }
};

Each call to the functor's operator() computes the model's prediction for a single data point. The current model parameters are specified in a TinyVector of appropriate length. The type T must be templated: normally, it is the same as DataType, but the nonlinearLeastSquares() function will temporarily replace it with a special number type that supports automatic differentiation (see vigra::autodiff::DualVector). In this way, the derivatives needed in the model's Taylor expansion can be computed automatically.

When the model is univariate (has a single scalar argument), the samples must be passed to nonlinearLeastSquares() in a pair 'x', 'y' of 1D MultiArrayViews (variant 1). When the model is multivariate (has a vector-valued argument), the 'x' input must be a 2D MultiArrayView (variant 2) whose rows represent a single data sample (i.e. the number of columns corresponds to the length of the model's argument vector). The number of rows in 'x' defines the number of data samples and must match the length of array 'y'.

The TinyVector 'model_parameters' holds the initial guess for the model parameters and will be overwritten by the optimal values found by the algorithm. The algorithm's internal behavior can be controlled by customizing the option object vigra::NonlinearLSQOptions.

The function returns the residual sum of squared errors of the final solution.

Usage:

#include <vigra/regression.hxx>
Namespace: vigra

Suppose that we want to fit a centered Gaussian function of the form

to noisy data 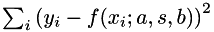, i.e. we want to find parameters a, s, b such that the residual 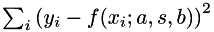is minimized. The model parameters are placed in a TinyVector<T, 3> p according to the rules
p[0] <=> a, p[1] <=> s and p[2] <=> b.
The following functor computes the model's prediction for a single data point x:

struct GaussianModel
{
    template <class T>
    T operator()(double x, TinyVector<T, 3> const & p) const
    {
        return p[0] * exp(-0.5 * sq(x / p[1])) + p[2];
    }
};

Now we can find optimal values for the parameters like this:

int size = ...;  // number of data points
MultiArray<1, double> x(size), y(size);    
...   // fill the data arrays

TinyVector<double, 3> p(2.0, 1.0, 0.5);  // your initial guess of the parameters
                                         // (will be overwritten with the optimal values)
double residual = nonlinearLeastSquares(x, y, p, GaussianModel());

std::cout << "Model parameters: a=" << p[0] << ", s=" << p[1] << ", b=" << p[2] << " (residual: " << residual << ")\n";